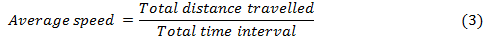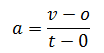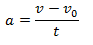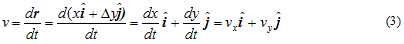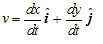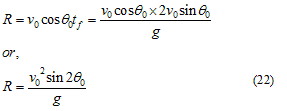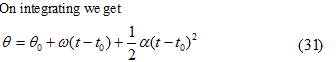Question: If you are riding on a train that speeds past other train moving in the same direction on adjacent train.It appears the other train is moving backward. Why?
Solution:
Your reference frame is that of the train you are riding. If you are traveling with a relatively constant velocity (not over a hill or around a curve or drastically changing speed), then you will interpret your reference frame as being at rest. Since you are moving forward faster than the other train, the other train is moving backwards relative to you. Seeing the other train go past your window from front to rear makes it look like the other train is going backwards. This is similar to passing a semi truck on the interstate out of a passenger window, it looks like the truck is going backwards.
Question:A package is dropped from the plane.Four People sitting in the plane make different statements about the package location when it hits the ground.Air resistance can be ignored
Person A: The package will fall behind the plane
Person B: The package remain below the plane until it hit the ground
Person C:The package move ahead of the plane
Person D: The package location will depend on the speed of the plane
Person B: The package remain below the plane until it hit the ground
Person C:The package move ahead of the plane
Person D: The package location will depend on the speed of the plane
We know that only one person is correct and three are wrong
Who are those three person’s
A) Person A,B,C
b) Person A,C,D
c) Person B,C,D
d) Person A,B,D
Who are those three person’s
A) Person A,B,C
b) Person A,C,D
c) Person B,C,D
d) Person A,B,D
Solution:
The package will have same horizontal velocity as of plane.The vertical velocity will be dictated by the force of gravity.
So it will cover the same horizontal distance as plane before hitting the ground.So Person B is correct
So it will cover the same horizontal distance as plane before hitting the ground.So Person B is correct
Question: Jack and Henry both are good swimmer and can swim with same speed in still water . They setoff across the river at the same time.
Jack moves straight across and Jack is pulled downstream by the current somewhat.Henry heads upstream at an angle so as to arrive at a point directly opposite to starting point .
Jack moves straight across and Jack is pulled downstream by the current somewhat.Henry heads upstream at an angle so as to arrive at a point directly opposite to starting point .
Who will cross the river first?
A) jack
A) jack
b) henry
c) Both Jack and Henry will cross the river in same time
Solution:
Both jack and henry need to cover the same “cross river” distance. The swimmer with the greatest speed in the “cross river” direction will be the one that reaches the other side first.The current has no bearing on the problem because the current doesn’t help either of the boats move across the river.
Thus the swimmer heading straight across will reach the other side first. All of his swiming effort has gone into crossing the river. For the upstream swimmer, some of his swimming effort goes into battling the current,and so his “cross river” speed will be only a fraction of his swimming speed.So Jack will come first
Thus the swimmer heading straight across will reach the other side first. All of his swiming effort has gone into crossing the river. For the upstream swimmer, some of his swimming effort goes into battling the current,and so his “cross river” speed will be only a fraction of his swimming speed.So Jack will come first
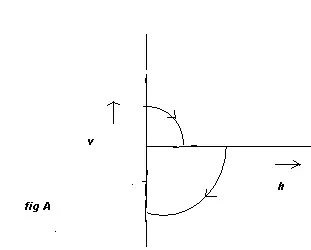
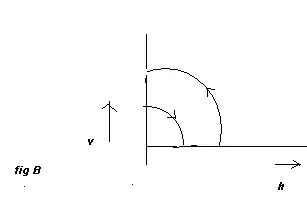
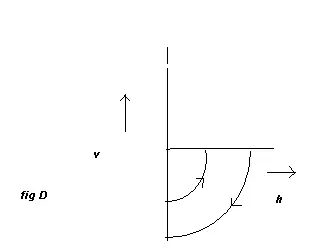
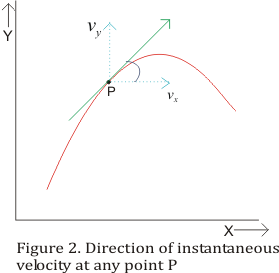
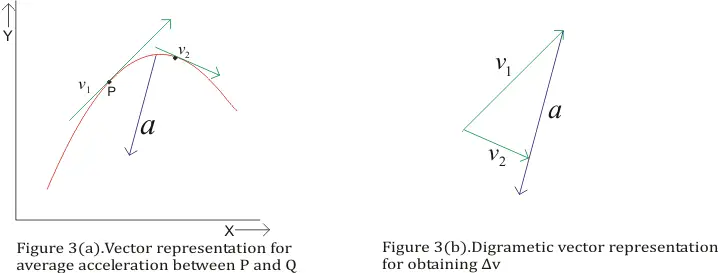
Question:
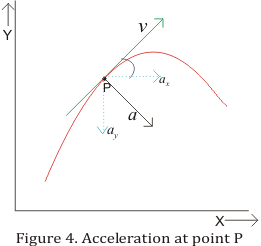
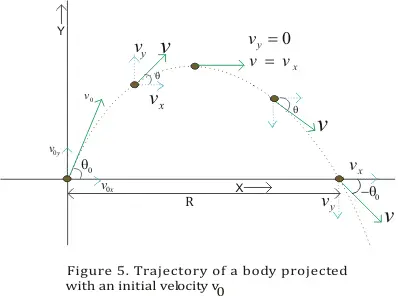
During projection motion,the velocity and acceleration vectors are acting in
different direction at different points.
different direction at different points.
Which of the following is true
a) v.a =0 at the topmost point
b) v.a < 0 during the upward journey
c) v.a > 0 during the downward journey
d) None of these
Solution:
During Upward journey
v=vxi+vyj
g=-gj
v.a < 0
At topmost point
v=vxi
g=-gj
v.a =0
During downward journey
v=vxi-vyj
g=-gj
v.a > 0